- Autor Matthew Elmers elmers@military-review.com.
- Public 2024-01-11 09:39.
- Última modificação 2025-01-24 09:33.
Neste artigo, tentaremos entender a penetração da armadura dos canhões dos navios de guerra Bayern, Rivenge e Pensilvânia, bem como a qualidade comparativa das armaduras alemãs, americanas e britânicas. É extremamente difícil fazer isso, porque os dados dos canhões americano de 356 mm, alemão de 380 mm e britânico de 381 mm são muito vagos e incompletos e às vezes se contradizem, mas tentaremos mesmo assim.
Qual é exatamente o problema? Vamos ver como a maioria dos fãs da história naval (e não só) compara a penetração da blindagem de certas armas. Por exemplo: em uma publicação dedicada, por exemplo, a encouraçados ingleses, há informações de que um projétil britânico de 381 mm da Primeira Guerra Mundial perfurou uma blindagem de 381 mm a uma distância de cerca de 70 cabos. Em outra edição, dedicada aos navios já "capitais" alemães - que um projétil alemão semelhante de 380 mm "dominou" blindagem de 350 mm com apenas 67,5 cabos. Parece resultar disso que o canhão inglês é mais poderoso - esta é precisamente a conclusão feita.
No entanto, na realidade, comparar dados como esse dessa forma é muito fácil de se complicar.
Os dados acima são obtidos como resultado de tiro real ou são calculados usando técnicas de penetração de armadura? Se esses forem os resultados do tiro real, as condições foram idênticas para as duas armas? Se a penetração da armadura foi obtida por cálculo, os mesmos métodos foram usados? Os dados obtidos são o resultado do trabalho de especialistas dos ministérios e departamentos relevantes, ou são o resultado de cálculos de historiadores que pegaram uma calculadora? É claro que no segundo caso a precisão será muito menor … Não é preciso ir muito longe para obter exemplos: tomemos a famosa monografia de S. Vinogradov, "Superdreadnoughts of the Second Reich" Bayern "e" Baden " No Apêndice nº 2, o respeitado historiador, junto com V. L. Kofman faz uma grande quantidade de cálculos para comparar as capacidades dos encouraçados Rivenge e do Bayern. Mas, infelizmente, basta olhar a tabela de parâmetros para canhões de 15 polegadas (p. 124) e veremos que, segundo os cálculos de autores respeitados, um canhão inglês de 381 mm com um ângulo de elevação de 20, 25 graus tem um alcance de apenas 105 cabos, ou seja, cerca de 19,5 mil m. Enquanto fontes estranhas para a mesma velocidade inicial (732 m / s) e um ângulo de elevação ligeiramente inferior (20 graus) fornecem distâncias significativamente maiores - 21, 3-21, 7 mil m. Claro, no entanto, esses desvios dos valores reais têm o efeito mais negativo sobre os resultados do cálculo.
Mas mesmo que as fontes apresentem resultados de cálculos de especialistas, cuja exatidão não há dúvida, surge outro fator que complica a comparação: o que interessa aqui é a qualidade da armadura. É claro que os mesmos britânicos, ao calcular a penetração da armadura ao projetar um encouraçado específico, usaram os indicadores correspondentes da armadura britânica, os alemães - respectivamente, alemão, etc. E as armaduras de diferentes países podem diferir em durabilidade, mas isso ainda é metade do problema: afinal, em um único país, a mesma armadura Krupp estava sendo constantemente aprimorada. Assim, verifica-se que os cálculos dos sistemas de artilharia, feitos, por exemplo, na Inglaterra, e aparentemente para a mesma armadura Krupp, mas feitos em momentos diferentes, podem revelar-se incomparáveis. E se somarmos a isso a quase completa ausência de trabalhos sérios sobre a evolução da caixa de blindagem em vários países do mundo …
Em geral, uma comparação mais ou menos confiável da penetração da armadura não é uma tarefa tão simples quanto pode parecer à primeira vista. E, de forma amigável, um leigo (que, sem dúvida, é o autor deste artigo), melhor não se ocupar desse assunto. Mas, infelizmente - para nosso profundo pesar, os profissionais de alguma forma não têm pressa em lidar com essas questões, então … como dizem, na ausência de papel selado, escrevemos em texto simples.
Claro, não é mais possível fazer testes em escala real dos sistemas de artilharia mencionados acima, então nosso destino são os cálculos. E se sim, então é necessário dizer pelo menos algumas palavras sobre as fórmulas de penetração da armadura. Se métodos de cálculo modernos são publicados, então apenas em edições fechadas e na literatura popular, a fórmula de Jacob de Marr é geralmente fornecida. É interessante que Professor da Academia Naval L. G. Goncharov, em seu livro de artilharia de 1932, chamou-a de fórmula de Jacob de Marr. Essa fórmula, junto com muitas outras, foi difundida no início do século passado e, devo dizer, é bastante precisa - talvez seja até a mais precisa entre as fórmulas semelhantes daqueles anos.
Sua peculiaridade reside no fato de não ser físico, ou seja, não é uma descrição matemática de processos físicos. A fórmula de De Marr é empírica, reflete os resultados do bombardeio experimental de ferro e armadura de aço-ferro. Apesar de sua "natureza não científica", a fórmula de de Marr mostrou uma melhor aproximação com os resultados reais do tiro e na armadura Krupp do que outras fórmulas comuns e, portanto, vamos usá-la para cálculos.
Os interessados encontrarão essa fórmula no apêndice deste artigo, mas não há necessidade de forçar todos os que estão lendo este material a entendê-la - isso não é necessário para entender as conclusões do artigo. Constatamos apenas que o cálculo utiliza conceitos muito simples e familiares a todos os interessados na história das frotas militares. Estes são a massa e o calibre do projétil, a espessura da armadura, o ângulo em que o projétil atinge a armadura, bem como a velocidade do projétil quando atinge a placa da armadura. No entanto, de Marr, é claro, não poderia se limitar aos parâmetros acima. Afinal, a penetração de um projétil depende não apenas de seu calibre e massa, mas também, em certa medida, de sua forma e da qualidade do aço de que é feito. E a espessura da placa da armadura, que o projétil é capaz de superar, depende, é claro, não apenas do desempenho do projétil, mas também da qualidade da armadura. Portanto, de Marr introduziu um coeficiente especial na fórmula, que, na verdade, é projetado para levar em conta as qualidades indicadas de uma armadura e um projétil. Este coeficiente aumenta com o aumento da qualidade da armadura e diminui com a deterioração da forma e da qualidade do projétil.
Na verdade, a principal dificuldade em comparar os sistemas de artilharia de diferentes países é justamente "repousar" neste mesmo coeficiente, que, no futuro, chamaremos simplesmente de (K). Teremos de encontrá-lo para cada uma das ferramentas acima - se, é claro, quisermos obter um resultado um tanto correto.
Então, vamos primeiro tomar dados bastante difundidos sobre a penetração da armadura do canhão alemão 380 mm / 45 "Bayern", segundo o qual o canhão a uma distância de 12.500 m (aqueles mesmos 67,5 cabos) poderia penetrar 350 mm de armaduras. Usamos uma calculadora balística para encontrar os parâmetros de um projétil de 750 kg, com uma velocidade inicial de 800 m / s no momento do impacto na armadura: verifica-se que tal projétil atingirá uma placa de armadura estritamente posicionada verticalmente em um ângulo de 10, 39 graus, com uma velocidade de 505, 8 m / s. Um pequeno aviso - doravante, quando falamos sobre o ângulo de impacto do projétil, queremos dizer o chamado "ângulo do normal". "Normal" é quando o projétil atinge o bonneplite estritamente perpendicular à sua superfície, ou seja, em um ângulo de 90 graus. Conseqüentemente, o projétil atingiu um ângulo de 10 graus.do normal significa que atingiu a laje em um ângulo de 80 graus. à sua superfície, desviando-se da "referência" 90 graus. em 10 graus.
Mas voltando à penetração da armadura da arma alemã. O coeficiente (K), neste caso, será aproximadamente (arredondado para o número inteiro mais próximo) igual a 2.083 - este valor deve ser considerado normal para armaduras da era da Primeira Guerra Mundial. Mas aqui surge um problema: o fato é que a fonte de dados sobre penetração de blindados é o livro "Navios da Capital Alemã da Segunda Guerra Mundial", onde o canhão 380 mm / 45 do Bayern foi comparado com o calibre principal do encouraçado "Bismarck". E não será que o cálculo levou em conta os indicadores da armadura Krupp, criada no intervalo entre as duas guerras mundiais, muito mais forte do que a que foi instalada em Bayenne, Rivenge e Pensilvânia? Além disso, a enciclopédia eletrônica navweaps relata que há evidências de que, a uma distância de 20.000 m, os projéteis alemães de 380 mm foram capazes de penetrar a blindagem de 336 mm, e estamos falando sobre a blindagem da era da Primeira Guerra Mundial.
Bem, acreditamos: a 20 km, o ângulo de incidência será de 23,9 graus, a velocidade do projétil na armadura é de 410,9 m / s, e o coeficiente (K) - alguns infelizes 1618, que não cabe na armadura valores de resistência em todas as épocas da Primeira Guerra Mundial. Um resultado semelhante geralmente traz a armadura Krupp de fabricação alemã mais próxima da resistência de armadura homogênea … Obviamente, os dados de navweaps contêm algum tipo de erro.
Vamos tentar então usar outra fonte de informação. Até agora, usamos os dados calculados, e agora tentaremos compará-los com os resultados de testes reais do canhão alemão 380 mm / 45: aqueles são dados por S. Vinogradov na monografia acima mencionada dedicada ao alemão navios de guerra.
Descreve as consequências de 3 disparos com projéteis perfurantes, contra placas de blindagem com espessura de 200, 290 e 450 mm, sendo esta última a mais interessante para nós: um projétil de 734 kg atingiu a placa de blindagem com um ângulo de 0 (isto é, a 90 graus da superfície) e a uma velocidade de 551 m / s puncionado 450 mm através da laje. Um resultado semelhante corresponde ao coeficiente (K) 1.913, mas, na verdade, será um pouco menor, porque os alemães encontraram seu projétil a até 2 530 m atrás do obstáculo que perfurou, e - em geral. Infelizmente, não tendo nenhum dado sobre quanto dessa distância o projétil voou pelo ar, quanto - "cavalgou" no solo, é absolutamente impossível determinar a energia armazenada por ele após a penetração da armadura.
Tomemos agora o sistema de artilharia britânico 381 mm / 42. Infelizmente, os dados sobre a penetração de sua armadura são bastante vagos: por exemplo, V. L. Kofman, há uma menção ao fato de que essas armas britânicas perfuraram armadura, a espessura de seu próprio calibre a uma distância de cerca de 70 cabos. Mas com que projétil e com que velocidade inicial? Tendo em conta que a referência consta da monografia dedicada ao cruzador de batalha "Hood", e se refere ao período da criação deste navio, pode-se supor que se trata de um casco de 871 kg. No entanto, outra questão surge aqui: a velocidade inicial oficial de tal projétil era de 752 m / s, mas alguns cálculos pelos britânicos foram realizados a uma velocidade inferior de 732 m / s, então que valor devemos tomar? No entanto, qualquer que seja a velocidade indicada que tomarmos, o coeficiente (K) irá flutuar dentro de 1.983 - 2.048, e isso é mais alto do que calculamos para o valor (K) para o canhão alemão. Pode-se supor que isso fala da superioridade da qualidade da armadura britânica em comparação com a alemã … ou será que a forma geométrica do projétil alemão era mais adequada para penetração? Ou talvez a questão toda seja que os dados de V. L. Kofman são valores calculados, mas, na prática, os projéteis britânicos alcançariam um resultado melhor?
Pois bem, temos à nossa disposição dados sobre os resultados do bombardeamento do encouraçado "Baden"

Então, um dos projéteis britânicos, atingindo um ângulo de 18 graus. a uma velocidade de 472 m / seg., "superou" a blindagem frontal de 350 mm da torre de calibre principal alemão. Esses dados são ainda mais valiosos porque, neste caso, não os britânicos, mas sim a blindagem alemã foi submetida a bombardeios, ou seja, os testes dos canhões 381 mm / 42 e 380 mm / 45 estão, portanto, em um único sistema de coordenadas.
Infelizmente, eles não nos ajudam muito. Se assumirmos que o projétil inglês perfurou a torre alemã, como dizem, “com o último resquício de força”, e se houvesse uma armadura de 351 mm, ela teria falhado, então seu (K) seria igual a 2.021. é interessante, aliás, que S. Vinogradov afirma que o projétil britânico, que penetrou na blindagem frontal de 350 mm da torre alemã, não foi posteriormente encontrado, mas na verdade o relatório afirma outra coisa - explodiu, e há um descrição de onde os fragmentos voaram na torre.
Claro, não temos fundamentos absolutos para supor que essa penetração foi o limite para um projétil de 381 mm, ou mesmo perto disso. Mesmo assim, de acordo com alguns indícios indiretos, pode-se supor que foi exatamente esse o caso. Outro acerto “dá uma dica” disso: um projétil britânico de 871 kg acertou uma barbete de 350 mm em um ângulo de 11 graus, embora tenha conseguido fazer um buraco na armadura com um diâmetro de 40 cm, não entrou na churrasqueira em si, explodindo no processo de superar a armadura. Nesse caso, o golpe ocorreu quase no centro do barbet, ou seja, a curvatura da placa da armadura, se teve alguma influência, foi mínima.
De tudo isso, pode-se tentar tirar algumas conclusões, mas, devido à fragilidade da base de evidências, elas, é claro, serão de natureza muito conjectural.
Conclusão 1: a armadura alemã durante a Primeira Guerra Mundial quase se equiparou à britânica em termos de durabilidade. Esta conclusão é válida se a declaração de V. L. Kofman que o canhão britânico 381 mm / 42 era capaz de penetrar blindagem igual ao seu calibre em 70 kbt, e se não nos enganássemos ao supor que a penetração de 350 mm da placa frontal da torre alemã em um ângulo de 18 graus e uma velocidade de 472 m / s … é o limite ou muito próximo do limite de penetração do projétil britânico de 381 mm.
Conclusão 2ª. Aparentemente, a forma e a qualidade do projétil alemão de 380 mm proporcionou-lhe uma penetração de blindagem melhor do que o inglês. Com base nos dados acima, podemos supor que o coeficiente (K) do projétil britânico de 381 mm ao disparar contra blindados alemães era de cerca de 2.000, enquanto o projétil alemão de 380 mm era de cerca de 1.900. Se o nosso primeiro estiver correto, concluímos que o A resistência da blindagem britânica e alemã é aproximadamente equivalente, é óbvio que a única razão para o coeficiente mais baixo (K) pode ser apenas o próprio projétil.
Por que uma concha alemã poderia ser melhor? Seu calibre é ligeiramente menor, em um milímetro, mas, é claro, isso dificilmente teria qualquer efeito significativo. O cálculo mostra que com a mesma massa (750 kg), uma mudança no calibre em 1 milímetro levará a um aumento na penetração da armadura em 1,03 milímetro. O projétil alemão também é mais curto - seu comprimento era de 3,5 calibre, enquanto o comprimento do britânico "Greenboy" é de 4 calibre. Pode ter havido outras diferenças também. Claro, a qualidade do aço do qual o projétil é feito desempenha um papel significativo aqui.
Agora vamos calcular a penetração da blindagem dos canhões alemães e britânicos para uma distância de 75 cabos - uma distância geralmente aceita para uma batalha decisiva, onde se poderia esperar acertos suficientes para destruir um navio inimigo da linha.
Na distância indicada, 871 kg de um projétil de canhão britânico 381 mm / 42, disparado a uma velocidade inicial de 752 m / s, atingiu a placa de armadura posicionada verticalmente em um ângulo de 13,05 graus, e sua velocidade "na placa" era 479,6 m / s … Com (K) igual a 2.000, segundo a fórmula de Jacob de Marr, a penetração da blindagem do projétil britânico era de 376,2 mm.
Quanto à casca alemã, tudo é um pouco mais complicado. Se nossa conclusão de que ele superou o inglês em termos de penetração de blindagem estiver correta, então as capacidades do canhão alemão 380 mm / 45 em 75 cabos foram muito próximas ao canhão inglês de quinze polegadas. A esta distância, o projétil alemão de 750 kg atingiu o alvo em um ângulo de 12,42 graus a uma velocidade de 482,2 m / se em (K) igual a 1.900, a penetração da armadura foi de 368,9 mm. Mas se o autor deste artigo ainda se engana, e para o canhão alemão vale a pena usar o mesmo coeficiente do canhão inglês, então as capacidades do projétil de 380 mm caem para 342,9 mm.
No entanto, segundo o autor, a penetração da armadura do projétil alemão é mais próxima de 368,9 mm (afinal, o tiro prático rendeu um coeficiente de 1.913, apesar do projétil ter voado então 2,5 km), mas a penetração da armadura do projétil inglês pode ser calculado ligeiramente inferior. Em geral, pode-se considerar que a uma distância de 75 cabos, os sistemas de artilharia britânico e alemão são bastante comparáveis em termos de penetração de blindagem.
Mas com o canhão americano 356 mm / 45, tudo ficou muito mais interessante. Os dados citados anteriormente para conchas pesando 680 kg devem ser considerados canônicos na literatura de língua russa.
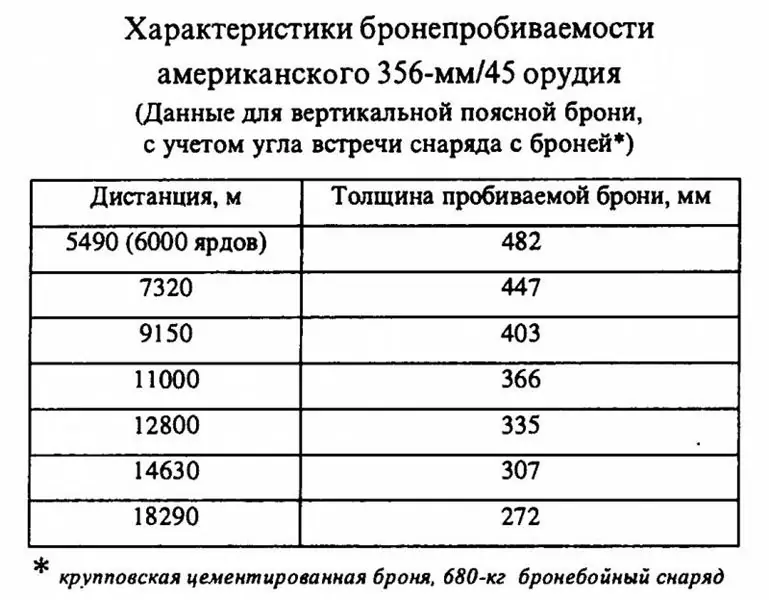
Na verdade, os valores indicados nele parecem levar a conclusões completamente óbvias: se mesmo as cápsulas de 680 kg que apareceram nos Estados Unidos depois de 1923 são inferiores em penetração de blindagem aos seus europeus de 380-381 mm " colegas ", então o que realmente falar sobre os primeiros projéteis de 635 kg, que foram equipados com artilharia de 356 mm de encouraçados americanos! São mais leves, o que significa que perdem velocidade mais rapidamente em vôo, enquanto sua velocidade inicial não ultrapassava os projéteis mais pesados e, em termos de formato e qualidade, a munição de 1923 deveria ter uma vantagem. Está claro como o dia que a "Pensilvânia" americana no momento da entrada em serviço era inferior em termos de penetração de blindagem aos encouraçados britânicos e alemães. Bem, é óbvio, não é?
Essa é exatamente a conclusão que o autor fez, considerando as capacidades dos canhões americanos de quatorze polegadas no artigo Encouraçados "Standard" dos Estados Unidos, Alemanha e Inglaterra. Americano "Pensilvânia". E então ele pegou uma calculadora …
O fato é que o cálculo segundo a fórmula de Marra mostrou que os canhões americanos 356-mm / 45 tinham a penetração da blindagem indicada na tabela com coeficiente (K) igual a 2.317! Em outras palavras, os projéteis americanos de 680 kg mostrados na tabela mostraram os resultados quando expostos a uma armadura que não foi criada na era da Primeira Guerra Mundial, mas em amostras muito posteriores e mais duráveis.
É difícil dizer o quanto a força da proteção da armadura aumentou no intervalo entre a primeira e a segunda guerra mundial. Em fontes em língua russa, há apenas referências breves e frequentemente contraditórias a esse problema, com base nas quais pode-se presumir que a resistência da armadura de Krupp aumentou em cerca de 20-25%. Assim, para os projéteis de grande calibre da era do Primeiro Mundo, o crescimento do coeficiente (K) será de 1.900 - 2.000 para 2.280 - 2.500, mas aqui deve ser lembrado que com um aumento na qualidade da proteção da armadura, é claro, a qualidade dos projéteis também aumentou e, portanto, para munições pesadas da Segunda Guerra Mundial (K) pode ser menor. Portanto, (K) no valor de 2.317 para projéteis do pós-guerra, naturalmente melhorado levando em consideração a experiência adquirida anteriormente, parece bastante orgânico, mas para a armadura da era da Segunda Guerra Mundial, não a primeira.
Mas ao definir o coeficiente (K) para os projéteis americanos de 680 kg no nível de 2.000, ou seja, trazendo a qualidade da proteção da armadura para a era da Primeira Guerra Mundial, para uma distância de 75 cabos teremos armadura penetração no nível de 393,5 mm, ou seja, maior do que a dos canhões de quinze polegadas britânicos e alemães!

A conversão para projétil de 635 kg dá uma correção muito insignificante - a calculadora balística mostrou isso a uma distância de 75 cabos, com um ângulo de incidência de 10, 82 graus. e a velocidade "na blindagem" 533, 2 m em (K) igual a 2.000, o projétil americano penetra na blindagem da era da Primeira Guerra Mundial, com 380 mm de espessura, isto é, significativamente mais do que seu próprio calibre!
Por outro lado, é bem possível que tal cálculo ainda não seja totalmente correto. O fato é que, segundo alguns relatos, o coeficiente (K) para uma mesma armadura diminui com o aumento do calibre do projétil. Assim, por exemplo, em nossos cálculos, o valor máximo (K) para o sistema alemão de artilharia 380 mm / 45, obtido por cálculo e publicado em fontes, é 2.083. Ao mesmo tempo, os cálculos para o alemão 305 mm / 50 canhões, que foram instalados em navios Kaiserlichmarine a partir dos Heligoland, os dados de fontes de penetração de blindados dão (K) ao nível de 2.145. Assim, é possível que os canhões de 356 mm / 45 (K) = 2.000 que tomamos para calcular a penetração da blindagem das armas americanas ainda é muito pequena.
Além disso, infelizmente, o autor não tem nenhuma "pista" para comparar a resistência da blindagem Krupp americana com suas contrapartes europeias. Não resta nada além de considerá-la equivalente à proteção de blindagem alemã e inglesa, embora isso, é claro, possa não ser o caso.
Vamos resumir todos esses dados um tanto caóticos. Levando em consideração os erros dos "métodos" utilizados nos cálculos, pode-se supor com alto grau de probabilidade que A penetração da blindagem da proteção blindada vertical dos canhões de calibre principal dos couraçados Rivenge, Bayern e Pensilvânia a uma distância de 75 cabos era aproximadamente a mesma e era de aproximadamente 365-380 mm.
Apesar de um monte de suposições, os dados à nossa disposição ainda nos permitem tirar algumas conclusões sobre a proteção de blindagem vertical. Mas com a quebra das barreiras horizontais, que são decks blindados, tudo fica muito mais complicado. O fato é que Jacob de Marr, infelizmente, não se preocupou em criar uma fórmula para determinar a força da defesa horizontal. A sua fórmula básica, adaptada aos modernos tipos de armadura, só é adequada para o cálculo de armaduras cimentadas com espessura superior a 75 mm. Esta fórmula é fornecida no Apêndice No. 1 deste artigo, e todos os cálculos anteriores no artigo foram feitos usando-a.
Mas os conveses dos navios daqueles anos eram protegidos não por blindagem cimentada (heterogênea), mas por blindagem homogênea, que carecia de uma camada superficial endurecida. Para tal armadura (mas - instalada verticalmente!), Uma fórmula diferente é usada, destinada a avaliar placas de armadura não cimentadas com uma espessura inferior a 75 mm, é fornecida no Apêndice No. 2.
Gostaria de observar que ambas as fórmulas são tiradas de uma fonte mais do que séria: “O curso da tática naval. Artillery and Armor 1932, autor - Professor da RKKA Naval Academy L. G. Goncharov, um dos maiores especialistas da URSS antes da guerra no campo da artilharia naval.
E, infelizmente, nenhum deles é adequado para avaliar a durabilidade da proteção horizontal. Se usarmos a fórmula para armadura cimentada, a uma distância de 75 cabos teremos penetração de armadura escassa: 46,6 mm para 381 mm / 42 britânicos, 39,5 mm para 380 mm / 45 alemães e 33,8 mm para 356 mm / 45 americanos armas. Se usarmos a segunda fórmula para armadura não cimentada, então obtemos que quando atingidos em um ângulo típico de uma distância de 75 cabos, todos os três sistemas de artilharia penetram facilmente na placa de armadura de 74 mm, após o que retendo um grande suprimento de energia cinética - por exemplo, o inglês 381 mm, um projétil para penetrar uma armadura desta espessura a uma distância de 75 cabos terá uma velocidade de 264,5 m / s, enquanto sua velocidade será de 482,2 m / s. Se ignorarmos a limitação da espessura da placa de blindagem, verifica-se que o projétil britânico de 381 mm, de acordo com a fórmula acima, é capaz de penetrar blindagem de convés com uma espessura de mais de 180 mm! O que, claro, é completamente impossível.
Se tentarmos nos referir aos resultados do teste do encouraçado classe Bayern, veremos que os projéteis britânicos perfurantes de 871 kg atingiram duas vezes a blindagem horizontal das torres, que tinham uma espessura de 100 mm em um ângulo de 11 graus, que corresponde a uma distância de 67,5 cabos para um projétil com velocidade inicial de 752 m / se 65 cabos - para um projétil com velocidade inicial de 732 m / s. Ambas as vezes a armadura não foi perfurada. Mas, em um caso, o projétil, ricocheteando, fez um sulco na armadura com 70 cm de profundidade, ou seja, a placa estava fortemente dobrada. E na segunda, embora a concha, novamente, ricocheteasse, a armadura não era apenas côncava em 10 cm, mas também rasgada.

A natureza similar do dano sugere que, embora a blindagem alemã de 100 mm fornecesse proteção nas distâncias indicadas, ela estava, senão no limite do possível, então muito próxima disso. Já o cálculo de acordo com a fórmula da armadura cimentada dá penetração da armadura de apenas 46,6 mm a uma distância maior, onde o ângulo de incidência será maior e, consequentemente, seria mais fácil para o projétil penetrar na armadura do convés. Ou seja, de acordo com a fórmula, verifica-se que o deck de 100 mm deveria ter brincadeira e com uma grande margem de segurança refletir conchas inglesas - porém, a prática não confirma isso. Ao mesmo tempo, de acordo com cálculos usando a fórmula para armadura não cimentada, verifica-se que os telhados do calibre principal de Baden deveriam ter sido perfurados facilmente e - com um grande suprimento de energia de projéteis - o que, novamente, não é em tudo confirmado pela prática.
Devo dizer que tais imprecisões nos cálculos têm uma explicação completamente lógica. Como dissemos antes, as fórmulas de de Marr não são uma descrição matemática de processos físicos, mas apenas uma fixação dos padrões obtidos ao testar armaduras. Mas a proteção de armadura vertical, não horizontal, foi testada, e não é de forma alguma surpreendente que os padrões neste caso simplesmente parem de funcionar: para armadura localizada horizontalmente, na qual os projéteis atingem em um ângulo muito pequeno de sua superfície, esses padrões, claro, são completamente diferentes.
O autor deste artigo encontrou opiniões "na Internet" de que as fórmulas de de Marr funcionam eficazmente em ângulos de desvio do normal não superiores a 60 graus, ou seja, de 30 graus à superfície da laje e mais. Pode-se presumir que essa avaliação está muito próxima da verdade.
Assim, devemos lamentar que o aparato matemático de que o autor dispõe não permite realizar cálculos confiáveis da resistência da proteção horizontal dos encouraçados Rivenge, Bayern e Pensilvânia. Diante do exposto, será difícil usar os dados sobre a penetração da armadura de armadura horizontal fornecidos em várias fontes - via de regra, todos eles se baseiam nos mesmos cálculos de acordo com as fórmulas de de Marr e estão incorretos.






