- Autor Matthew Elmers [email protected].
- Public 2023-12-16 22:30.
- Última modificação 2025-01-24 09:33.

Neste artigo, tentaremos determinar a durabilidade da armadura russa da Primeira Guerra Mundial. Esta questão é extremamente difícil, porque é extremamente mal abordada na literatura. E o ponto é este.
É bem sabido que, no final do século XIX, as principais potências marítimas na construção de navios de guerra passaram a usar armaduras feitas pelo método Krupp. Mas isso não significa de forma alguma que, desde então, a blindagem dos navios de todos esses países se tornou equivalente.
Acontece que a "receita clássica" da armadura de Krupp (também conhecida como "qualidade 420", criada em 1894) não permaneceu inalterada, mas melhorou. Pelo menos por países como Inglaterra e Alemanha. Mas como exatamente ele se aperfeiçoou, e a que resultados vieram os mestres da armadura de vários poderes - isso, infelizmente, não sei com certeza.
Julgamento por fogo
A resistência ao projétil da armadura russa pode ser determinada com precisão aceitável, graças ao bombardeio experimental do antigo encouraçado "Chesma", reclassificado como "navio excluído nº 4". Um compartimento experimental foi criado na nave, copiando a proteção de várias partes dos encouraçados da classe Sevastopol, e para a pureza do experimento também foi equipado com muitos dispositivos que tais partes deveriam ter. Assim, por exemplo, tubos de vapor (que ali passavam em navios de guerra), armas de fogo, dispositivos de controle de fogo e fios elétricos, etc. foram instalados nas casamatas.

Em seguida, o compartimento experimental foi disparado com várias munições de calibre de 6 a 12 polegadas, incluindo, é claro, os mais recentes projéteis perfurantes e altamente explosivos de 305 mm. Dito isso, os relatórios de teste são muito completos, como deveria ser nesses casos. Eles contêm não apenas uma descrição das consequências de um acerto, mas também a velocidade do projétil no momento em que atinge a armadura, bem como o ângulo em que o projétil e a armadura se encontram.
Tudo isso nos permite calcular a resistência da blindagem russa em relação aos mais recentes projéteis domésticos de 470,9 kg, segundo a mesma fórmula de Jacob de Marr, que já citei várias vezes antes. Mas vou citar novamente, para que o caro leitor não tenha que se preocupar com os artigos anteriores. A relação entre a qualidade do projétil e a durabilidade da armadura nesta fórmula é descrita pelo coeficiente "K". Além disso, quanto maior esse coeficiente, mais forte é a blindagem.

Uma certa dificuldade em avaliar a armadura russa é criada pelo fato de que os projéteis foram testados principalmente, e não a resistência final da armadura de proteção dos últimos encouraçados. Parece ser - qual é a diferença? Mas, na verdade, é muito significativo. Quando os projéteis estão sendo testados, o interesse está na destruição confiável da armadura nas principais distâncias de batalha. Quando a armadura é testada, há interesse nas condições finais nas quais ela ainda pode proteger o navio.
No entanto, as estatísticas de acertos no "navio excluído nº 4" ainda nos permitem tirar algumas conclusões.
Sobre atirar em armadura de 250 mm
Infelizmente, acertos na armadura de 125 mm ou menos não são de interesse para nós - em todos os casos, descobriu-se que ou a energia do projétil era mais do que suficiente para penetrá-lo, ou os ângulos de impacto eram tão pequenos que deram um ricochete. Em outras palavras, para determinar a durabilidade da armadura, as estatísticas de acertos na armadura de 125 mm e abaixo são inúteis.
Uma questão diferente é atingir as espessas blindagens de 225 mm e 250 mm, que veremos mais de perto.
Comecemos com 250 mm de blindagem, que protegia as paredes da torre de comando da "nave excluída nº 4". No total, 13 tiros foram disparados contra esta casa do leme, mas alguns deles foram disparados contra seu telhado, e outros por granadas explosivas. Os projéteis perfurantes foram disparados contra blindagem de 250 mm apenas 5 vezes.
O tiro mais poderoso foi o nº 6 (numerado de acordo com relatórios de teste). Um projétil perfurante de armadura de 305 mm atingiu a placa da armadura em um ângulo de 80 ° (10 ° do normal) a uma velocidade de 557 m / s. Um projétil teria uma velocidade semelhante de 470,9 kg a uma distância de apenas 45 cabos. É verdade que o ângulo de desvio do normal seria menor - 6, 18 °.
Claro, o projétil perfurou a armadura. Para segurá-lo, seria necessária uma armadura com um "K" de mais de 2.700. E esse é um valor exorbitante, mesmo para os padrões das armaduras muito mais avançadas da Segunda Guerra Mundial. Os cálculos feitos por mim mostram que à distância o mod de canhão 305 mm / 52 russo. 1907 poderia penetrar a placa de armadura de 433 mm Krupp "qualidade 420".
Os 4 tiros restantes foram disparados em igualdade de condições. A velocidade do projétil na armadura era de 457 m / s, os ângulos de encontro com o obstáculo eram de cerca de 80 ° (desvio dos 10 ° normais). De acordo com meus cálculos, os projéteis russos teriam essa velocidade a uma distância de 75 cabos, mas o ângulo de encontro com um obstáculo seria pior - 76,1 ° (desvio do normal - 13, 89 °). Em tais condições, de acordo com os cálculos acima, 285,7 mm de armadura Krupp penetraram (com K = 2000). Mas, na realidade, tudo acabou não tão inequívoco.
Durante a tomada 11, tudo correu bem. O perfurante venceu a placa de blindagem de 250 mm, atingiu a parede oposta da casa do leme e já explodiu, fazendo um buraco no ponto de impacto de 100 mm de profundidade. Quando o tiro # 10 foi disparado, a armadura também foi quebrada. Mas não está totalmente claro quando exatamente o estouro do shell ocorreu - isso não é indicado no relatório. Mas, aparentemente, isso aconteceu dentro da torre de comando, porque a força da explosão arrancou as placas de blindagem do telhado, e a placa adjacente de 250 mm foi simplesmente arrancada das montagens e implantada.

Assim, com este tiro, a penetração da rede e a passagem do projétil devem ser contadas para a proteção da armadura como um todo.
Mas quando o tiro # 9, um pequeno incidente ocorreu - o projétil atingiu a armadura diretamente oposto ao chão de 70 mm. Como resultado, a placa de blindagem de 250 mm foi perfurada e até mesmo seu canto, de aproximadamente 450x600 mm de tamanho, quebrou e um buraco de 200 mm de comprimento foi encontrado no piso de 70 mm. Portanto, pode-se argumentar que, também neste caso, o projétil não apenas perfurou a blindagem, mas o fez com uma quantidade decente de energia, que foi suficiente para danificar uma chapa de aço blindada de 70 mm localizada horizontalmente.
Consequentemente, em quatro de cinco acertos, os projéteis perfurantes de armadura russos mostraram o resultado esperado, confirmado por cálculos de Marr. Mas quando o tiro # 7, uma coisa estranha aconteceu - o projétil atingiu a placa de armadura exatamente da mesma maneira, no mesmo ângulo de 80 ° e com a mesma velocidade de 457 m / s, mas não perfurou a armadura, explodindo durante sua passagem. Como resultado, um buraco com uma profundidade de 225-250 mm apareceu: apenas "fragmentos de um projétil com até 16 kg de peso" entraram.
Vemos que de 4 acertos de projéteis perfurantes de armadura de 305 mm, que deveriam ter penetrado armadura com mais de 285 mm de espessura, apenas 3 foram penetrações "limpas". Em um caso, o projétil explodiu ao passar pela armadura, embora devesse não foi.
Qual é a razão deste fiasco? Talvez seja a própria casca? Vamos supor que um fusível com defeito funcionou prematuramente. Mas outra interpretação também é possível: o fato é que a penetração de uma armadura por um projétil é de natureza probabilística. Ou seja, não existe tal coisa que, por exemplo, se, de acordo com a fórmula de Jacob de Marr, a espessura máxima da armadura perfurada por um projétil em certas condições for de 285 mm, então a armadura de 286 mm não será penetrada pelo projétil em qualquer caso. Pode muito bem acontecer. E vice-versa - quebre nas mesmas condições contra armaduras de menor espessura.
Em outras palavras, a fórmula de Jacob de Marr em si (ou qualquer outra análoga a ela) não tem exatidão farmacológica. Na realidade, existem distâncias inteiras nas quais um projétil atingindo uma placa de armadura em um certo ângulo e a uma certa velocidade pode penetrar na armadura com um certo grau de probabilidade, mas isso não pode ser calculado usando fórmulas de penetração de armadura geralmente aceitas. E pode muito bem ser que, no caso do tiro nº 7, a probabilidade acima mencionada funcionou.
Assim, em minha opinião, os resultados da tacada # 7 são aleatórios e não devem ser levados em consideração. E a armadura dos encouraçados russos com uma espessura de 250 mm não resistiu a ser atingida por 470,9 kg de um projétil a uma velocidade de 457 m / se um ângulo de encontro com um obstáculo de cerca de 80 °. De acordo com de Marr, verifica-se que o coeficiente "K" da blindagem russa, neste caso, deve ser inferior a 2.228. Mas quanto?
Em minha opinião, a resposta pode ser obtida analisando as consequências do tiro nº 11. O projétil perfurou uma placa de 250 mm, atingiu a parede oposta e fez um buraco de 100 mm ali. Portanto, podemos assumir que a penetração máxima da armadura do projétil russo de 470,9 kg com os parâmetros acima foi de 250 mm da armadura cimentada de Krupp. E 100 mm adicionais de armadura homogênea não cimentada separados.
Por que é homogêneo? O fato é que, como você sabe, a armadura cimentada consiste, por assim dizer, em duas camadas. A de cima é muito forte, mas ao mesmo tempo frágil, e então mais macia, mas uma armadura mais viscosa começa. O projétil, atingindo a placa de blindagem de 250 mm, atingiu a camada “macia e viscosa” de dentro da casa do leme, que em suas qualidades é bastante semelhante à blindagem homogênea, ao invés de cimentada.
Além disso, deve-se levar em conta que estou calculando o coeficiente "K" para um projétil que atravessa a armadura como um todo e explode atrás dela. Mas no caso do tiro nº 11, não foi o que aconteceu - o projétil, rompendo 250 mm da armadura cimentada de Krupp e acertando a parte de trás da segunda placa, não perfurou a armadura, mas explodiu, e apenas levando para dentro conta a energia da explosão, conseguiu fazer um buraco de 100 mm. Assim, o cálculo de "armadura homogênea 250 mm cimentada + 100 mm" pode ser considerado feito em suposições que são obviamente desfavoráveis para a armadura. Assim, o resultado obtido pode ser considerado o mínimo abaixo do qual a resistência da armadura Krupp de fabricação russa não terá.
E então o cálculo é muito simples. A velocidade do projétil, como já foi dito várias vezes acima, é de 457 m / s, o ângulo de desvio do normal quando atinge a placa de blindagem de 250 mm é de 10 °. Ao passar por essa armadura, o projétil vai "girar" e atingir a segunda placa já em um ângulo de 90 °, ou seja, 0 ° de desvio do normal. Isso decorre do diagrama nº 9 ““Curso de tática naval. Artilharia e blindagem "L. G. Goncharov, dado na página 132. Onde, além da força dos projéteis no impacto, há um gráfico do giro do projétil ao passar pela armadura, dependendo do ângulo de encontro com essa armadura.
A proporção de resistência da armadura da armadura russa homogênea e cimentada é desconhecida para mim. Mas, segundo G. Evers, a armadura cimentada alemã teve um coeficiente "K" 23% maior que a homogênea. E, provavelmente, para a armadura russa, essa proporção também é verdadeira. Além disso, deve-se ter em mente que ao passar por uma placa de blindagem de 250 mm, o projétil perderá sua capa perfurante. Isso, ao contrário, levará a um aumento na blindagem homogênea "K" em 15%.
No cálculo da velocidade de um projétil para penetrar uma placa homogênea de 100 mm, foi utilizada a mesma fórmula que para uma placa cimentada de 250 mm, apenas o coeficiente "K" foi alterado. Eu sei que L. G. Goncharov recomendou o uso de uma fórmula diferente fornecida em seu livro para armadura homogênea. Mas ela, segundo ele, é projetada para placas de blindagem mais finas que 75 mm. Afinal, temos 100 mm. Além disso, de acordo com G. Evers, o uso da fórmula de Jacob de Marr acima também é aplicável para armaduras homogêneas.
De acordo com os resultados do cálculo do "K" da armadura russa cimentada, o valor de 2005. Agora vamos ver se houve algum caso durante o tiroteio que refutou esse resultado.
Sobre disparar em armadura de 225 mm
Apenas 2 cartuchos perfurantes foram disparados contra a armadura de 225 mm. Além disso, a velocidade do projétil no momento do contato com a armadura chegava a 557 m / s - velocidade que o projétil deveria ter a uma distância de 45 cabos. É verdade que o ângulo de encontro com a armadura era muito desvantajoso - um desvio de 65 ° ou 25 ° do normal. Mas mesmo neste caso, para suportar o impacto de 470,9 kg do projétil, a placa de blindagem deveria ter um coeficiente "K" acima de 2 690. O que, claro, é completamente impossível. Em outras palavras, ao disparar com tais parâmetros, até mesmo a armadura da era da Segunda Guerra Mundial teve que ser perfurada com um grande suprimento de energia do projétil.
E com o tiro # 25, foi exatamente o que aconteceu. O projétil perfurou facilmente a placa de armadura de 225 mm (ela nem mesmo rompeu, mas simplesmente quebrou um pedaço de 350x500 mm dela) e, em seguida, atingiu o chanfro, que consistia em uma armadura de 25 mm em um metal de 12 mm substrato, e fez um furo 1x1,3 nele m. A localização exata da explosão do projétil não foi estabelecida. Mas presumiu-se que ele entrou na sala de máquinas e já explodiu lá. Em outras palavras, o resultado foi exatamente o que se esperaria de tal golpe.
Mas com o segundo assalto (tiro nº 27), tudo se revelou incompreensível. O projétil desviou-se do ponto de mira. E, como diz o relatório, "acerte a borda superior da armadura." O resultado da foto será mais fácil de citar a partir do documento:
“O projétil fez um buraco na armadura com cerca de 75 mm de profundidade e cerca de 200 mm de largura e, rasgando a borda saliente da camisa com um quadrado, explodiu sem diminuir a velocidade aqui, emitindo uma fumaça preta. Casemate No. 2 não foi danificado."
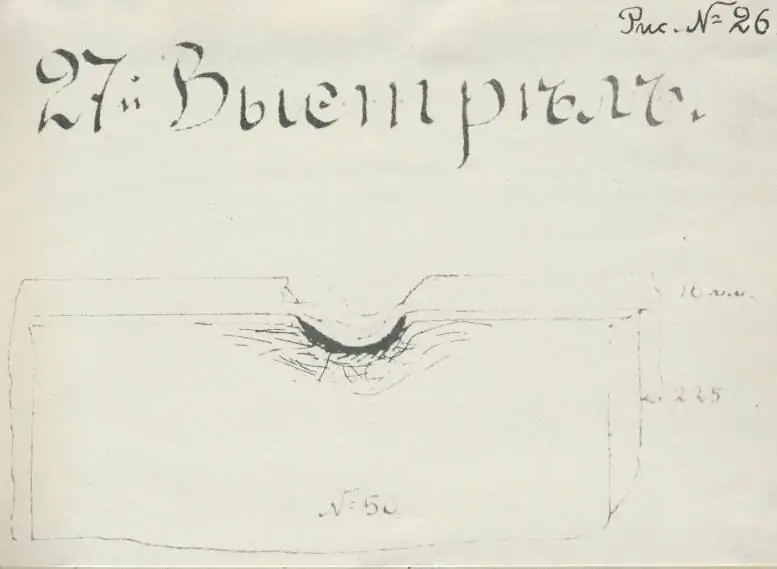
Não está totalmente claro o que poderia ter acontecido aqui. Principalmente porque não está claro onde exatamente o projétil atingiu. Para começar, "borda" é em si um conceito extensível, uma vez que pode ser usado, entre outras coisas, para significar "a borda de algo". Ou seja, nem mesmo está claro se a linha central do projétil atingiu a superfície vertical ou horizontal da placa de armadura.
Mas na presença de um fusível de alta qualidade, danos muito maiores seriam esperados de qualquer uma dessas opções. Se o projétil atingiu o plano vertical da armadura, ele deveria ter colapsado em toda a sua profundidade, não em 75 mm. Se o impacto caiu na parte horizontal, então por que, então, o ângulo do obstáculo que atinge cerca de 65 ° é registrado no relatório? O projétil não caiu do céu sobre a superfície horizontal da laje de 225 mm, foi disparado em um ângulo de 65 ° com a superfície vertical, o que significa que deveria ter sido de 25 ° em relação à horizontal. Nesse caso, você pode esperar uma recuperação. Ou (no caso de uma explosão de um projétil) dano ao deck de blindagem horizontal de 37,5 mm adjacente à borda superior da placa de blindagem de 225 mm. Mas nada disso aconteceu.
Na minha opinião, a falha foi um projétil defeituoso que colapsou com o impacto, razão pela qual a explosão não saiu com força total. Ou, talvez, um fusível defeituoso que detonou "alto explosivo" no momento em que o projétil tocou a armadura. Também é possível que o projétil não estivesse com defeito, mas sim colapsado porque o ângulo formado pelas duas superfícies da placa da armadura funcionava como uma espécie de “cutelo”. Formalmente, o projétil não penetrou nas placas de 225 mm. Mas em conexão com a extrema incomum das consequências do golpe, na minha opinião, a razão não deve ser procurada nas qualidades ultra-altas da placa de armadura.
Consequentemente, os resultados do bombardeio das placas de blindagem de 225 mm do "vaso excluído nº 4" não confirmam ou refutam nossa conclusão anterior.
No entanto, houve outros testes marcantes de projéteis e armaduras domésticas que ocorreram em 1920. Aqui, o objetivo era completamente diferente. O compartimento experimental foi construído sob o comando do czar-pai para determinar o esquema de proteção ideal para os futuros encouraçados russos. Mas em 1917, algo deu errado com a autocracia na Rússia. E os projetos de construção de encouraçados passaram para a categoria de projeção. No entanto, os testes foram realizados, e incluindo - usando conchas de 305 mm 470, 9 kg. Os resultados são muito interessantes. Mas falaremos sobre isso no próximo artigo.
Mas o que eu gostaria de observar separadamente é a presença de uma estranheza gritante nos testes. O fato é que eles superestimaram deliberadamente as distâncias do fogo de artilharia.
Assim, por exemplo, para tiros em armadura de 225 mm com projéteis perfurantes, é indicado que a distância correspondente aos parâmetros do projétil é de 65 cabos. Mas isso não é verdade - a uma velocidade de 557 m / s com um desvio do normal de 25 °, um projétil de 305 mm deveria ter penetrado na armadura cerca de 8% mais espesso do que ao disparar em 65 cabos, onde a velocidade do projétil seria foram 486,4 m, e a deflexão do normal - 10, 91 °.
Claro, pode-se suspeitar de um erro banal nos cálculos do autor do artigo, ou seja, eu. Mas como então entender o tiro na torre de comando - aqui nos documentos a velocidade do projétil é indicada todos iguais 557 m / s de desvio do normal - apenas 10 °, mas a distância é considerada a mesma, ou seja, 65 cabos ! Em outras palavras, verifica-se que a "distância adequada" foi indicada de forma alguma sem levar em consideração o ângulo de incidência, apenas em termos da velocidade do projétil?
No entanto, esta versão é facilmente verificável. De acordo com meus cálculos, a velocidade do projétil para 60 cabos é 502,8 m / s, e para 80 cabos é 444 m / s. Ao mesmo tempo, os dados sobre o alcance de tiro de canhões 305 mm / 52 fornecidos por L. G. Goncharov ("Curso de tática naval. Artilharia e blindagem", p. 35), mostram para essas distâncias 1671 e 1481 pés / s, respectivamente, ou seja, traduzidas no sistema métrico - 509 e 451 m / s.
Assim, podemos assumir que minha calculadora ainda dá um certo erro para baixo, no valor de 6-7 m / s. Mas é óbvio que 557 m / s para 65 cabos e 457 m / s para 83 cabos estão fora de questão aqui.
E mais um fato que te faz pensar. Como você pode ver, um total de 7 tiros de projéteis perfurantes de armadura de 305 mm foram disparados em uma armadura de 225-250 mm. Ao mesmo tempo, as condições de disparo eram tais que a blindagem especificada teve que romper com uma margem considerável. No entanto, em condições reais de tiro, mesmo que ao alcance, apenas em cinco casos de sete projéteis perfuraram a armadura. E apenas 4 projéteis passaram por dentro.






